栈
栈(stack)是限制插入和删除只能在一个位置上进行的表,该位置是表的末端叫做栈的顶(top),对栈的基本操作有 push(进栈)和 pop(出栈),前者相当于插入,后者则是删除最后插入的元素。
栈的另一个名字是 LIFO(先进后出)表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| public class StackTest {
int len;
int[] elems;
int top = -1;
public StackTest(int len) {
this.len = len;
this.elems = new int[len];
}
public boolean isFull(){
return top == len - 1;
}
public boolean isEmpty(){
return top == -1;
}
public int pop() {
if (isEmpty()) {
throw new RuntimeException("empty stack");
}
int val = this.elems[top];
top--;
return val;
}
public void push(int i) {
if (isFull()) {
throw new RuntimeException("full stack");
}
top++;
elems[top] = i;
}
}
|
队列
像栈一样,队列(queue)也是表。然而使用队列时插入在一端进行而删除在另一端进行,遵守先进先出的规则。所以队列的另一个名字是(FIFO)。
队列的基本操作是入队(enqueue):它是在表的末端(队尾(rear)插入一个元素。出队(dequeue):出队他是删除在表的开头(队头(front))的元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| public class QueueTest {
int rear = -1;
int front = -1;
int size;
int[] elems;
public QueueTest(int size) {
this.size = size;
this.elems = new int[size];
}
public boolean isEmpty() {
return rear == front;
}
public boolean isFull() {
return (rear + 1) % this.size == front;
}
public int dequeue() {
if (isEmpty()) {
throw new RuntimeException("empty queue");
}
this.front = (this.front + 1) % this.size;
return this.elems[this.front];
}
public void enqueue(int val) {
if (isFull()) {
throw new RuntimeException("full queue");
}
this.rear = (this.rear + 1) % this.size;
this.elems[this.rear] = val;
}
}
|
散列表
散列过程
- 通过散列函数计算记录的散列地址,并按此散列地址存储该记录
- 查找时,我们通过同样的散列函数计算记录的散列地址,按此散列地址访问该记录
散列函数构造方法
直接定址法
数字分析法
折叠法
除法散列法
乘法散列法
随机数法
平方取中法
处理散列冲突的方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| public class HashTest {
KeyValue[] elements;
int size = 6;
public HashTest() {
this.elements = new KeyValue[size];
}
public void put(String key,String value) {
int index = key.hashCode() % this.size;
KeyValue element = this.elements[index];
if (element != null) {
while (element.next != null) {
element = element.next;
}
KeyValue newKv = new KeyValue(key, value);
newKv.setNext(element);
this.elements[index] = newKv;
}else {
element = new KeyValue(key, value);
this.elements[index] = element;
}
}
public String get(String key) {
int index = key.hashCode() % this.size;
KeyValue element = this.elements[index];
while (!element.getKey().equals(key)) {
element=element.next;
}
return element.getValue();
}
public static class KeyValue {
private String key;
private String value;
private KeyValue next;
public String getKey() {
return key;
}
public void setKey(String key) {
this.key = key;
}
public String getValue() {
return value;
}
public void setValue(String value) {
this.value = value;
}
public KeyValue getNext() {
return next;
}
public void setNext(KeyValue next) {
this.next = next;
}
public KeyValue(String key, String value) {
this.key = key;
this.value = value;
this.next = null;
}
}
}
|
链表
定义:链表是一种递归的数据结构,他或者为空(null),或者是指向一个结点(node)的引用,该结点含有一个泛型的元素和一个指向另一条链表的引用。是一种线性表,但是他不是按线性顺序存取数据。链表在内存不是连续分配的
链表的类型
树
树是 n (n >= 0) 个节点的有限集。 n = 0 时 我们称之为空树, 空树是树的特例。
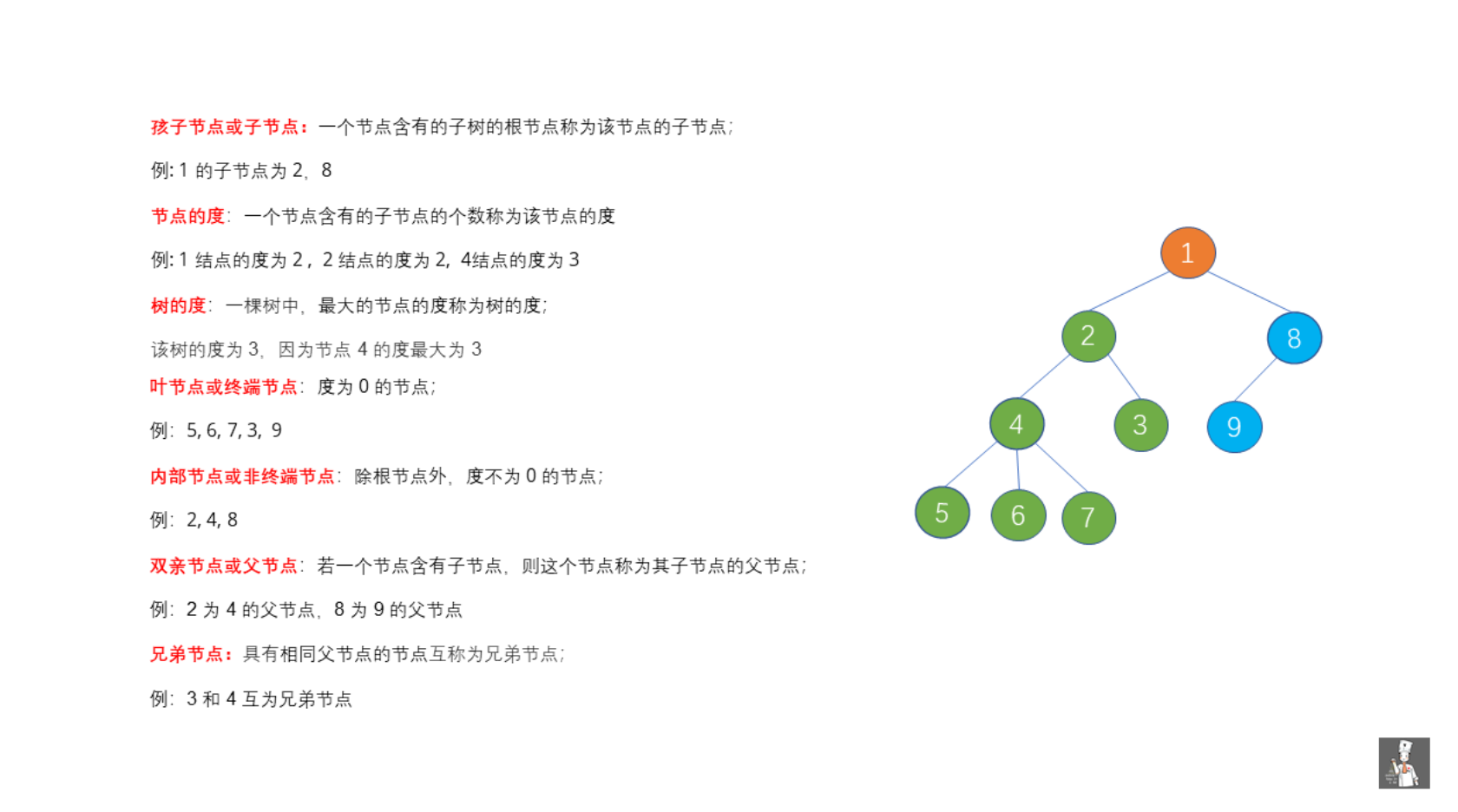
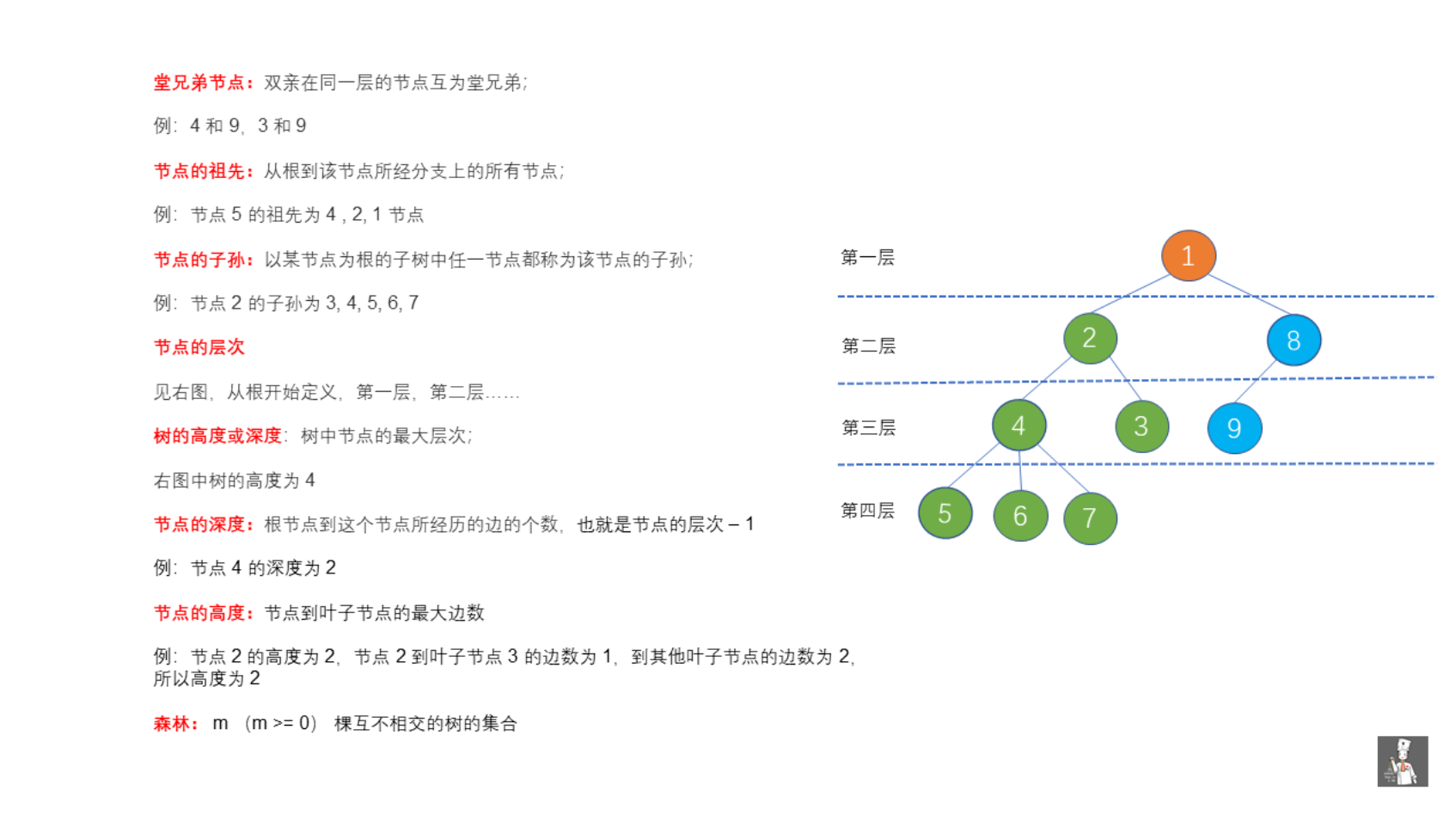
整理源自algorithm-base/二叉树基础.md at main · chefyuan/algorithm-base · GitHub
二叉树
- 每个节点最多有两棵子树,也就是说二叉树中不存在度大于 2 的节点,节点的度可以为 0,1,2。
- 左子树和右子树是有顺序的,有左右之分。
- 假如只有一棵子树 ,也要区分它是左子树还是右子树
特殊的二叉树
满二叉树
满二叉树:在一棵二叉树中,所有分支节点都存在左子树和右子树,并且所有的叶子都在同一层
完全二叉树
叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。
斜二叉树
斜二叉树也就是斜的二叉树,所有的节点只有左子树的称为左斜树,所有节点只有右子树的二叉树称为右斜树.
遍历
前序遍历
1
2
3
4
5
6
7
8
9
| public TreeNode traverse(TreeNode root, List<Integer> arr) {
if (root == null) {
return root;
}
arr.add(root.val);
traverse(root.left, arr);
traverse(root.right, arr);
return root;
}
|
中序遍历
1
2
3
4
5
6
7
8
9
| public TreeNode traverse(TreeNode root, List<Integer> arr) {
if (root == null) {
return root;
}
traverse(root.left, arr);
arr.add(root.val);
traverse(root.right, arr);
return root;
}
|
后序遍历
1
2
3
4
5
6
7
8
9
| public TreeNode traverse(TreeNode root, List<Integer> arr) {
if (root == null) {
return root;
}
traverse(root.left, arr);
traverse(root.right, arr);
arr.add(root.val);
return root;
}
|
层级遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> list = new ArrayList<>();
if (root == null) {
return list;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
List<Integer> temp = new ArrayList<>();
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode treeNode = queue.poll();
if(treeNode.left!=null) queue.offer(treeNode.left);
if(treeNode.right!=null) queue.offer(treeNode.right);
temp.add(treeNode.val);
}
list.add(temp);
}
return list;
}
|

